180421 Practical Contest

比赛链接

题目	A	B	C	D	E
通过	√	√	√	√	√

其实是去年 ICPC 的组题，但是还是很有练习价值的。顺便复习了一下之前已经快要忘记的的内容。

Potassium 的题解请点我跳转。

A - Rikka with Intersections of Paths

题解

两个树上的链若有交点，则交点必然是两个链中至少一个链的 LCA。因此对于每个点，统计通过这个点的链数 \(n\) 与该点为 LCA 的链数 \(m\)，用容斥原理即可得到以该点为交点的链组合方式为 \(C_n^k-C_{n-m}^k\)。

代码

点击显示 / 隐藏

#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;

typedef long long ll;
const int N=300000+5,LEN=20,MOD=1000000007;

int pa[N][LEN],dep[N];
vector<int> a[N];
int n,m,lim;

ll QPow(ll bas,int t){
    ll ret=1; bas%=MOD;
    for(;t;t>>=1,bas=bas*bas%MOD)
        if(t&1)ret=ret*bas%MOD;
    return ret;
}

ll Inv(ll x){
    return QPow(x,MOD-2);
}

void DFS4LCA(int u,int _pa=0){
    pa[u][0]=_pa;
    dep[u]=dep[_pa]+1;

    for(int i=1;i<LEN;i++)
        pa[u][i]=pa[pa[u][i-1]][i-1];
    for(int i=0;i<a[u].size();i++)
        if(a[u][i]!=_pa)
            DFS4LCA(a[u][i],u);
}

int LCA(int u,int v){
    if(dep[u]<=dep[v])swap(u,v);

    for(int i=LEN-1;i>=0;i--)
        if(dep[pa[u][i]]>=dep[v])
            u=pa[u][i];

    if(u==v)return u;

    for(int i=LEN-1;i>=0;i--)
        if(pa[u][i]!=pa[v][i])
            u=pa[u][i],v=pa[v][i];

    return pa[u][0];
}

int cnt[N],lca[N],lcas[N];		//cnt of LCA;
int l[N],r[N];
ll ans;

ll fac[N],inv[N];

ll C(int a,int b){		//C(a,b)	(a>=b)
    if(a<b)return 0;
    else return fac[a]*inv[b]%MOD*inv[a-b]%MOD;
}

void DFS(int u,int _pa=0){
    for(int i=0;i<a[u].size();i++)
        if(a[u][i]!=_pa){
            DFS(a[u][i],u);
            cnt[u]+=cnt[a[u][i]];
        }
}

void Init(){
    for(int i=1;i<=n;i++){
        a[i].clear();
        cnt[i]=lcas[i]=0;
    }
    ans=0;
}

int main(){
    fac[0]=inv[0]=1;
    for(int i=1;i<N;i++){
        fac[i]=fac[i-1]*i%MOD;
        inv[i]=Inv(fac[i]);
    }

    int nCase; scanf("%d",&nCase);
    while(nCase--){
        scanf("%d%d%d",&n,&m,&lim);
        Init();

        for(int i=1;i<n;i++){
            int u,v; scanf("%d%d",&u,&v);
            a[u].push_back(v);
            a[v].push_back(u);
        }

        for(int i=1;i<=m;i++)
            scanf("%d%d",&l[i],&r[i]);

        DFS4LCA(1);
        for(int i=1;i<=m;i++){
            lca[i]=LCA(l[i],r[i]);
            lcas[lca[i]]++;
            cnt[l[i]]++;cnt[r[i]]++;
            cnt[lca[i]]--;cnt[pa[lca[i]][0]]--;
        }
        DFS(1);

        for(int i=1;i<=n;i++){
            ans=(ans+C(cnt[i],lim))%MOD;
            ans=(ans-C(cnt[i]-lcas[i],lim))%MOD;
        }

        printf("%lld\n",(ans+MOD)%MOD);
    }

    return 0;
}

B - Misunderstood … Missing

题解

注意到每次的操作虽然具有后效性，但是不具有前效性，因此可以从后往前 DP。DP 中需要用一个维度记录当前位置 \(i\) 之后所有采取攻击操作的位置 \(a_k\) 与当前位置的距离之和 \(\sum_k (a_k-i)\)，以此计算操作 2 对 \(D\) 增加造成的总贡献。

需要滚动数组。

代码

点击显示 / 隐藏

#include<iostream>
#include<cstring>
using namespace std;

typedef long long ll;
const int N=100+5;
ll f[2][N][N*N];
ll a[N],b[N],c[N];

int main(){
    int nCase; cin>>nCase;
    while(nCase--){
        int n; cin>>n;
        for(int i=1;i<=n;i++)
            cin>>a[i]>>b[i]>>c[i];
            
        memset(f[(n+1)&1],-1,sizeof(f[(n+1)&1]));
        f[(n+1)&1][0][0]=0;

        for(int i=n+1;i>1;i--){
            int o=i&1;
            memset(f[o^1],-1,sizeof(f[o^1]));

            for(int j=0;j<=(n-i+1);j++){
                int p=n-i+1;
                for(int k=(1+j)*j/2;k<=(2*p-j+1)*j/2;k++){
                    if(f[o][j][k]==-1)continue;
                    //a
                    f[o^1][j+1][k+j+1]=max(f[o^1][j+1][k+j+1],f[o][j][k]+a[i-1]);
                    //b
                    f[o^1][j][k+j]=max(f[o^1][j][k+j],f[o][j][k]+b[i-1]*k);
                    //c
                    f[o^1][j][k+j]=max(f[o^1][j][k+j],f[o][j][k]+c[i-1]*j);
                }
            }
        }

        ll ans=0;
        for(int j=0;j<=n;j++){
            for(int k=(1+j)*j/2;k<=(2*n-j+1)*j/2;k++)
                ans=max(ans,f[1][j][k]);
        }

        cout<<ans<<endl;
    }


    return 0;
}

C - Mediocre String Problem

题解

可以将所求的串拆成 \(aba'\) 的形式，其中 \(a'\) 为 \(a\) 的反串，\(b\) 是一个回文串。因此可以对 \(s\) 中的每一个下标 \(i\)，统计从 \(i\) 开始向左能与 \(t\) 的前缀的反串匹配的最长长度 \(n\)，与以 \(i+1\) 为左端点的回文串个数 \(m\)，则这个点对答案的贡献为 \(nm\)。

第一个可以采用 Hash 在 \(\mathcal{O} (n\log n)\) 内完成（采用 ExKMP 可以达到 \(\mathcal{O} (n)\)），第二个可以用 Manacher。

学习了一下选择模数和基底的姿势，不要选择一些比较容易卡的数（比如常见大质数 \(1000000007\) 和 ull 自然溢出，后者被证明可以被 \(2^{13}\) 级别的串卡掉 ¹）。选择的原则是，模数用一个尽可能大的质数，基底选择一个具有一定规模的、能够让 Hash 值比较均匀分布的数为佳。这个页面给出了一些模数的选择方式。

虽然 ull 自然溢出的方式非常地快，但是也非常容易被卡。如果空间时间足够的话，采用双 Hash 是比较保险的行为。

~~所以说要用膜术打败模数，选择某个特殊 8 位质数一定可以过~~

代码

点击显示 / 隐藏

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

typedef long long ll;
typedef unsigned long long ull;
const int N=1000000+5,G=299213;

struct Hash{
    ull prod[N],powG[N];
    int len;

    void Build(char s[]){
        int len=strlen(s+1);
        for(int i=1;i<=len;i++)
            prod[i]=(prod[i-1]*G+s[i]-'a'+1);
        
        powG[0]=1;
        for(int i=1;i<=len;i++)
            powG[i]=powG[i-1]*G;	
    }

    ull Query(int l,int r){
        return prod[r]-prod[l-1]*powG[r-l+1];
    }
};

Hash hs,ht;

int LCS(int pos,int L,int R){
    while(L<R){
        int M=(L+R)/2;
        if(hs.Query(pos,pos+M-1)==ht.Query(1,M))
            L=M+1;
        else R=M;
    }
    return L-1;
}

int lcs[N],plin[N];		//palindrome
int f[2*N];

void Manacher(char t[],int n){
    static char s[2*N]; 
    static int cnt[2*N];
    
    memset(cnt,0,sizeof(cnt));
    for(int i=1;i<=n;i++){
        s[i*2-1]=t[i];
        s[i*2]=1;
    }
    s[0]=2,s[n*2]=3;

    int cur=f[0]=0,idx=0;
    for(int i=1;i<=2*n;i++){
        int& j=f[i]; j=0;
        if(cur-i>=0&&2*idx-i>=0)j=min(f[2*idx-i],cur-i);
        while(s[i-j-1]==s[i+j+1])j++;
        if(i+j>cur)cur=i+j,idx=i;
        
        cnt[max(0,i-j)]++;
        cnt[i+1]--;
    }

    for(int i=1;i<=2*n;i++){
        cnt[i]+=cnt[i-1];
        if(i&1)plin[i/2+1]=cnt[i];
    }
}

char s[N],t[N],i_s[N];

int main(){
    //freopen("C.in","r",stdin);

    scanf("%s%s",s+1,t+1);
    int n=strlen(s+1),m=strlen(t+1);
    for(int i=1;i<=n;i++)
        i_s[n-i+1]=s[i];

    hs.Build(i_s); ht.Build(t);
    for(int i=1;i<=n;i++)
        lcs[n-i+1]=LCS(i,0,min(n-i+1+1,m+1));
    Manacher(s,n);

    ll ans=0;
    for(int i=1;i<n;i++)
        ans+=1LL*lcs[i]*plin[i+1];
    printf("%lld",ans);

    return 0;
}

D - Magic Potion

题解

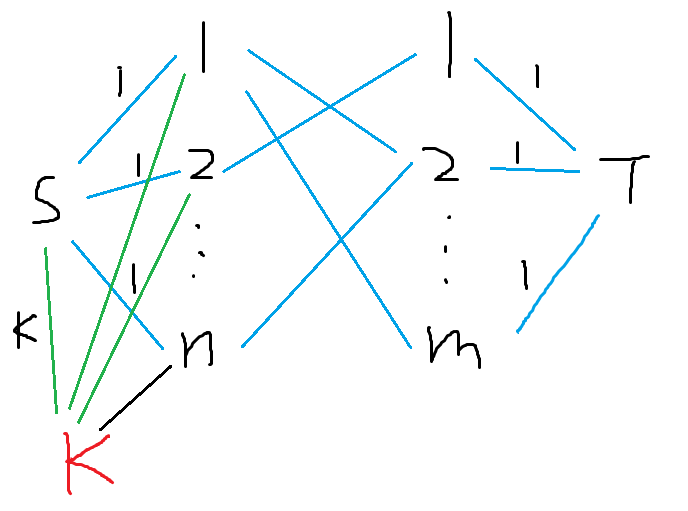
魔性构图。如果不设置 \(K\) 点，而是给每个点都连接流量为 \(2\) 的边，则会出现攻击了 2 次的人数大于 \(k\) 的情况，因此这种情况是不可行的。

代码

点击显示 / 隐藏

//19:38
#include<iostream>
#include<vector>
#include<deque>
#include<queue>
#include<cstring>
using namespace std;

const int N=500+5,INF=0x3f3f3f3f;

struct Dinic{
    const static int V=N*2;
    struct Edge{int v,res;};
    vector<Edge> edg;
    vector<int> a[V];
    int st,ed;

    void AddEdge(int u,int v,int cap){
        edg.push_back((Edge){v,cap});
        edg.push_back((Edge){u,0});
        int siz=edg.size();
        a[u].push_back(siz-2);
        a[v].push_back(siz-1);
    }

    int dep[V];
    bool BFS(){
        memset(dep,-1,sizeof(dep));
        dep[st]=0; 
        queue<int> q; q.push(st);

        while(!q.empty()){
            int u=q.front(); q.pop();
            for(int i=0;i<a[u].size();i++){
                Edge& e=edg[a[u][i]];
                if(dep[e.v]==-1&&e.res>0){
                    q.push(e.v),dep[e.v]=dep[u]+1;
                }
            }
        }

        return dep[ed]!=-1;
    }

    int cur[V];
    int DFS(int u,int minF){
        if(u==ed||minF==0)return minF;

        int tmpF,sumF=0;
        for(int& i=cur[u];i<a[u].size();i++){
            Edge& e=edg[a[u][i]];
            if( dep[e.v]==dep[u]+1 && (tmpF=DFS(e.v,min(e.res,minF)))>0 ){
                e.res-=tmpF; edg[a[u][i]^1].res+=tmpF;
                sumF+=tmpF; minF-=tmpF;
            }
            if(minF==0)break;
        }

        return sumF;
    }

    int MaxFlow(){
        int ret=0;
        while(BFS()){
            memset(cur,0,sizeof(cur));
            ret+=DFS(st,INF);
        }
        return ret;
    }
};

Dinic sol;

int main(){
    int n,m,q; cin>>n>>m>>q;
    for(int i=1;i<=n;i++){
        int p; cin>>p;
        while(p--){
            int idx; cin>>idx;
            sol.AddEdge(i,n+idx,1);
        }
        sol.AddEdge(0,i,1);
        sol.AddEdge(n+m+1,i,1);
    }
    sol.AddEdge(n+m+1,0,q);
    for(int i=n+1;i<=n+m;i++)
        sol.AddEdge(i,n+m+2,1);
    
    sol.st=n+m+1,sol.ed=n+m+2;
    cout<<sol.MaxFlow();

    return 0;
}

E - Prime Game

题解

分别对每个数 \(a_i\) 的质因数 \(p_i\) 考虑对所有 \((l,r)\) 的贡献，则显然 \(p_i\) 无法做贡献的情况是 \((l,r)\) 区间中不含有 \(p_i\)，因此区间总数量 \(C_{n+1}^2\) 需要减去这部分。最后统计一下即可。

代码

点击显示 / 隐藏

#include<iostream>
#include<cstdio>
#include<vector>
#include<ctime>
using namespace std;

typedef long long ll;
const int N=1000000+5;
bool notPri[N]; int pri[N];
vector<int> fac[N];

void Eratosthenes(){
    for(int i=2;i*i<N;i++){
        if(notPri[i])continue;
        for(int j=i*2;j<N;j+=i)
            notPri[j]=1;
    }

    for(int i=2;i<N;i++)
        if(notPri[i]==0){
            pri[++pri[0]]=i;
            for(int j=i;j<N;j+=i)
                fac[j].push_back(i);
        }
}

int pre[N];

int main(){
    Eratosthenes();

    ll ans=0;
    int n; scanf("%d",&n);
    for(int i=1;i<=n;i++){
        int a; scanf("%d",&a);
        for(int j=0;j<fac[a].size();j++){
            int v=fac[a][j];
            ans-=1LL*(i-pre[v])*(i-pre[v]-1)/2;
            pre[v]=i;
        }
    }

    for(int i=1;i<N;i++)
        if(pre[i]){
            ans+=1LL*(n+1)*n/2;
            ans-=1LL*(n-pre[i]+1)*(n-pre[i])/2;
        }

    printf("%lld",ans);

    return 0;
}

https://blog.csdn.net/wyfcyx_forever/article/details/39925891↩